Przykład
Hierarchiczną analizę skupień można wykonywać dla obiektów, które opisujemy za pomocą wielu różnych cech, np. szkoły – ilość uczniów ubiegających się o przyjęcie, wyniki egzaminów końcowych, ilość absolwentów, którzy znaleźli pracę bądź dostali się do szkoły wyższego szczebla, itd. Jednak ze względu na przejrzystość wykonywanych obliczeń przytoczymy przykład, w którym rozpatrzymy tylko 2 cechy opisujące dany obiekt.
Rozpatrzmy przypadek 10 rybnickich gimnazjów. Tabela przedstawia zestawienie średnich wyników egzaminu gimnazjalnego z części humanistycznej oraz matematyczno-przyrodniczej. Dane pobrano z serwisu http://www.edukacja.rybnik.eu/.
| SZKOŁA | Część humanistyczna | Część matematyczno-przyrodnicza |
| G01 | 26,5 | 24,0 |
| G02 | 26,3 | 24,9 |
| G03 | 23,6 | 19,5 |
| G04 | 23,9 | 22,7 |
| G05 | 18,3 | 17,4 |
| G06 | 21,2 | 20,7 |
| G07 | 26,3 | 23,2 |
| G10 | 24,5 | 22,8 |
| G11 | 23,9 | 21,4 |
| G12 | 22,4 | 18,8 |
Aby odpowiedzieć na pytanie, które ze szkół prezentują podobny poziom nauczania (ucznioweie zdają egzaminy końcowe na podobnym poziomie) wykonamy hierarchiczną analizę skupień.
Dane wyrażone są w tych samych jednostkach oraz skalach (w obu częściach egzaminu można było zdobyć 50 punktów). Ponadto zmienność wyników (odchylenie standardowe) jest zbliżona – 2,4 punktu dla części humanistycznej oraz 2,3 punktu dla części matematyczno-przyrodniczej. Zatem nie jest konieczna standaryzacja danych.
Licząc odległości (euklidesowe) pomiędzy szkołami ze względu na średnie wyniki egzaminu gimnazjalnego otrzymamy macierz:
| G01 | G02 | G03 | G04 | G05 | G06 | G07 | G10 | G11 | G12 | |
| G01 | 0,0 | 0,9 | 5,4 | 2,9 | 10,5 | 6,2 | 0,8 | 2,3 | 3,7 | 6,6 |
| G02 | 0,9 | 0,0 | 6,0 | 3,3 | 11,0 | 6,6 | 1,7 | 2,8 | 4,2 | 7,2 |
| G03 | 5,4 | 6,0 | 0,0 | 3,2 | 5,7 | 2,7 | 4,6 | 3,4 | 1,9 | 1,4 |
| G04 | 2,9 | 3,3 | 3,2 | 0,0 | 7,7 | 3,4 | 2,5 | 0,6 | 1,3 | 4,2 |
| G05 | 10,5 | 11,0 | 5,7 | 7,7 | 0,0 | 4,4 | 9,9 | 8,2 | 6,9 | 4,3 |
| G06 | 6,2 | 6,6 | 2,7 | 3,4 | 4,4 | 0,0 | 5,7 | 3,9 | 2,8 | 2,2 |
| G07 | 0,8 | 1,7 | 4,6 | 2,5 | 9,9 | 5,7 | 0,0 | 1,8 | 3,0 | 5,9 |
| G10 | 2,3 | 2,8 | 3,4 | 0,6 | 8,2 | 3,9 | 1,8 | 0,0 | 1,5 | 4,5 |
| G11 | 3,7 | 4,2 | 1,9 | 1,3 | 6,9 | 2,8 | 3,0 | 1,5 | 0,0 | 3,0 |
| G12 | 6,6 | 7,2 | 1,4 | 4,2 | 4,3 | 2,2 | 5,9 | 4,5 | 3,0 | 0,0 |
Widać, że najbliższe pod względem osiąganych przez uczniów wyników są gimnazja Nr 4, oraz Nr 10. Te dwa obiekty zakwalifikujemy zatem do pierwszego klastra. Środek ciężkości dla nowo utworzonego skupienia będzie następujący:
| SZKOŁY (klastry) | Część humanistyczna | Część matematyczno-przyrodnicza |
| G01 | 26,5 | 24,0 |
| G02 | 26,3 | 24,9 |
| G03 | 23,6 | 19,5 |
| G04, G10 | 24,2 | 22,8 |
| G05 | 18,3 | 17,4 |
| G06 | 21,2 | 20,7 |
| G07 | 26,3 | 23,2 |
| G11 | 23,9 | 21,4 |
| G12 | 22,4 | 18,8 |
Macierz odległości dla nowopowstałych 8 obiektów wygląda następująco:
| G01 | G02 | G03 | G04, G10 | G05 | G06 | G07 | G11 | G12 | |
| G01 | 0,0 | 0,9 | 5,4 | 2,6 | 10,5 | 6,2 | 0,8 | 3,7 | 6,6 |
| G02 | 0,9 | 0,0 | 6,0 | 3,0 | 11,0 | 6,6 | 1,7 | 4,2 | 7,2 |
| G03 | 5,4 | 6,0 | 0,0 | 3,4 | 5,7 | 2,7 | 4,6 | 1,9 | 1,4 |
| G04, G10 | 2,6 | 3,0 | 3,4 | 0,0 | 8,0 | 3,7 | 2,1 | 1,4 | 4,4 |
| G05 | 10,5 | 11,0 | 5,7 | 8,0 | 0,0 | 4,4 | 9,9 | 6,9 | 4,3 |
| G06 | 6,2 | 6,6 | 2,7 | 3,7 | 4,4 | 0,0 | 5,7 | 2,8 | 2,2 |
| G07 | 0,8 | 1,7 | 4,6 | 2,1 | 9,9 | 5,7 | 0,0 | 3,0 | 5,9 |
| G11 | 3,7 | 4,2 | 1,9 | 1,4 | 6,9 | 2,8 | 3,0 | 0,0 | 3,0 |
| G12 | 6,6 | 7,2 | 1,4 | 4,4 | 4,3 | 2,2 | 5,9 | 3,0 | 0,0 |
Kolejny klaster utworzą gimnazja o numerach 1 oraz 7. Środek ciężkości tego klastra wyniesie:
Postępowanie to powtarzamy aż do uzyskania jednego klastra zawierającego wszystkie elementy.
W przedostatnim kroku dostajemy macierz odległości:
| G01, G02, G04, G07, G11,G10 | G03,G06,G12 | G05 | |
| G01,G02,G04, G07, G11,G10 | 0,0 | 4,597 | 9,2 |
| G03,G06,G12 | 4,597 | 0,0 | 4,604 |
| G05 | 9,2 | 4,604 | 0,0 |
Klaster obejmujący trzy gimnazja (nr 3, nr 6 i nr 12) jest bliższy grupie szkół o nr 1, 2, 4, 7, 10 i 11. Zatem te dwa obiekty łączymy w jeden klaster.
W kolejnym, ostatnim kroku wszystkie szkoły utworzą jedno skupisko. Ostatecznie wybór ilości klastrów zależy jedynie od wykonującego analizy.
W naszym przypadku optymalnym rozwiązaniem wydaje się być podział gimnazjów na 4 grupy:
- Nr 1, Nr 2 oraz Nr 7 (gimnazja najlepsze)
- Nr 4, Nr 10 oraz Nr 11
- Nr 3, Nr 6 oraz Nr 12
- Nr 5 (gimnazjum najsłabsze)
Przy takim podziale maksymalna odległość pomiędzy elementami jednej grupy nie przekracza 2,7.
Przedstawiona metoda nie jest jedyną metodą łączenia skupisk podobnych elementów. Zamiast metody wykorzystującej środek ciężkości, równie dobrze moglibyśmy wykorzystać np. metodę, w której liczona jest średnia odległość pomiędzy punktami każdego z klastrów.
W wyniku zastosowania tej metody otrzymalibyśmy identyczne skupiska (różniłyby się jednak obliczone odległości pomiędzy skupiskami).
Graficzna interpretacja analizy wykonanej tą metodą wyglądałaby następująco (dendrogram):
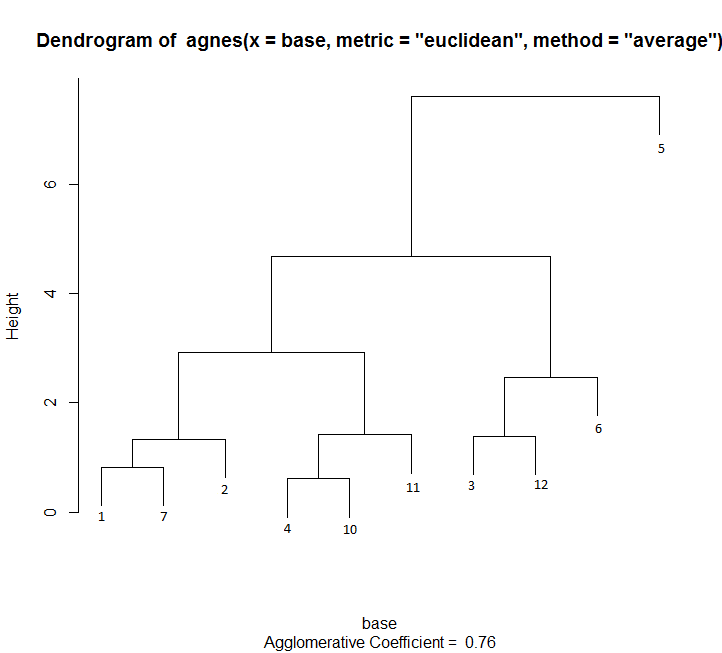
Rysunek wygenerowany za pomocą programu R 2.15.2
Na osi „Height” możemy odczytać średnie odległości pomiędzy elementami skupiska.
