Test U Manna-Whitneya
Test ten jest odpowiednikiem klasycznego testu t-Studenta dla prób niepowiązanych. Miarą tendencji centralnej dla tego testu jest nie średnia jak w przypadków testów t, a mediana.
Hipotezy alternatywną i zerową możemy zapisać następująco:
(próby pochodzą z jednej populacji)
(próby pochodzą z różnych populacji)
Statystyka testowa dla testu U Manna-Whitneya wyraża się wzorem:
gdzie:
- ,
- - suma reng elementów z pierwszej próby,
- - liczności odpowiednio pierwszej i drugiej próby.
Obszar krytyczne dla ustalonego odczytujemy z tablic rozkładu normalnego standardowego. Dla tak postawionych hipotez jest to obszar obustronny.
Przykład:
W ramach badania adherencji terapeutycznej u pacjentów ze stabilną chorobą wieńcową chorych poproszono m.in. o odpowiedź na takie 2 pytania:
- Jaka jest subiektywna ocena pacjenta pojawiających się dolegliwości bólowych (wg wizualnej skali analogowej VAS, gdzie 0 – brak bólu, 10 – ból najsilniejszy)?
- Czy pacjent regularnie przyjmuje zlecone przez lekarza leki?
Odpowiedzi na obydwa pytania uzyskano od 1148 pacjentów z rozpoznaniem choroby wieńcowej.
| Pytanie 2 Pytanie 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Suma |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nie | 4 | 26 | 50 | 75 | 93 | 73 | 64 | 32 | 13 | 0 | 3 | 433 |
| Tak | 20 | 56 | 106 | 134 | 138 | 114 | 86 | 40 | 19 | 1 | 1 | 715 |
| Suma | 24 | 82 | 156 | 209 | 231 | 187 | 150 | 72 | 32 | 1 | 4 | 1148 |
Czy istnieje związek pomiędzy regularnym zażywaniem zleconych leków a subiektywną oceną pojawiających się dolegliwości bólowych? W szczególności, czy u pacjentów wykazujących się adherencją terapeutyczną w zakresie regularnego przyjmowania leków oceny stopnia nasilenia bólu są niższe?
Weryfikację hipotezy o braku istotnych statystycznie różnic w rozkładach subiektywnych ocen nasilenia bólu u pacjentów w obu grupach przeprowadzimy za pomocą testu U Manna-Whitneya.
Najniższą ocenę 0 wskazało 24 pacjentów, stąd rangę tej oceny obliczamy jako średnią arytmetyczną liczb całkowitych z przedziału [1,24]. Wyniesie ona .
Ranga oceny 1 będzie równa średniej arytmetycznej 82 kolejnych rang poczynając od 25 a kończąc na 106: .
Analogicznie obliczamy rangi dla kolejnych wartości ocen otrzymując wyniki:
| Ocena | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ranga | 12,5 | 65,5 | 184,5 | 367 | 587 | 796 | 964,5 | 1075,5 | 1127,5 | 1144 | 1146,5 |
Suma rang dla pacjentów nie stosujących leków regularnie wyniesie:
.
Stąd otrzymujemy:
.
Wartość statystyki testowej wyniesie:
.
Przy takiej wartości statystyki hipotezę zerową mówiącą, że obie grupy pacjentów nasilenie bólowe oceniają tak samo, odrzucimy nawet dla bardzo wysokiego poziomu istotności , gdzie .
Z prawdopodobieństwem rzędu 99,9% możemy stwierdzić, że pacjenci przyjmujący leki zgodnie z zaleceniem lekarza oceniają nasilenie pojawiających się dolegliwości bólowych jako mniejsze.
Zależność tę przedstawiono graficznie na wykresie pudełkowym Min - Q1 (kwartyl dolny) –Me (mediana) - Q3 (kwartyl górny) - Max.
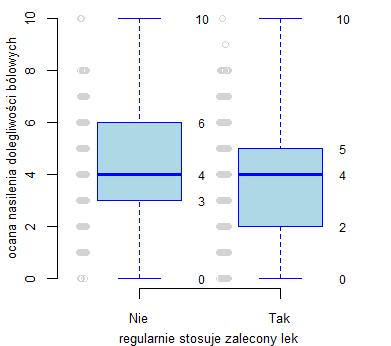
Wykres wygenerowano za pomocą programu R 2.15.2
Test U Manna-Whitneya jest powszechnie stosowany w różnego rodzaju analizach. Obok zastosowań medycznych, wykorzystywany jest m.in. w badaniach socjodemograficznych, marketingowych, badaniach opinii i wielu innych. Ze względu na brak konieczności spełnienia kłopotliwego założenia o normalności rozkładów, jest on prawdopodobniej najczęściej stosowanym testem jednorodności rozkładów.



 Kontakt
Kontakt





 (+48) 666069834
(+48) 666069834
 statystyka@biostat.com.pl
statystyka@biostat.com.pl




