Metoda CART
1. Drzewa klasyfikacyjne i regresyjne
Proces decyzyjny można zaprezentować graficznie przy pomocy drzew decyzyjnych wykorzystywanych m.in. w data mining jako sposób budowy modeli prognostycznych i opisowych. Przy ich pomocy w oparciu o pomiary zmiennych objaśniających dany obiekt jest przypisywany do klasy zmiennej zależnej.
Idea drzew opiera się na rekursywnym podziale danych na coraz to mniejsze sterty w celu jak najlepszego dopasowania. Początkowo próbka (węzeł macierzysty, korzeń) dzielona jest na dwa lub więcej podzbiorów (węzły potomne). Natomiast węzeł optymalny wyszukuje się na podstawie wszystkich punktów węzłowych dla każdej zmiennej. Następnie proces jest powtarzany dla każdego węzła potomnego, a te podczas dzielenia traktowane są jak węzły macierzyste. Węzeł, którego nie można już podzielić nazywamy liściem, bądź węzłem końcowym, a liczbę liści - wielkością drzewa.
Do rozwiązywania problemów zarówno regresyjnych, jaki i klasyfikacyjnych służy metoda CART (ang. Classification and Regression Trees). Metoda ta powstała w roku 1984. Opiera się na dwóch typach drzew:
-
Drzewa klasyfikacyjne - służą porządkowaniu klas, charakteryzuje je kategoryczna zmienna docelowa;

Rysunek 1: Idea drzew klasyfikacyjnych -
Drzewa regresyjne - służą do przewidywania wartości zmiennej docelowej, charakteryzuje je zmienna docelowa typu ciągłego.

Rysunek 2: Idea drzew regresyjnych
Konstrukcja algorytmu CART ma postać ciągu pytań, na które odpowiedzi determinują kolejne pytania, bądź kończą etap. W wyniku otrzymujemy strukturę drzewa, która w węzłach końcowych nie zawiera już pytań, lecz same odpowiedzi.
Czy kandydat został przyjęty do pracy

Rysunek 3: Drzewo decyzyjne - przykład
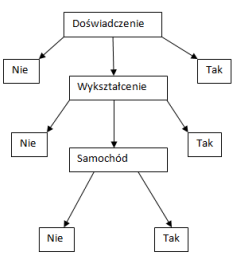
Rysunek 3: Drzewo decyzyjne - przykład
Zasada działania algorytmu CART polega na tym, że rozszczepianie danych w węzłach opiera się na jednej zmiennej decyzyjnej, a podział zostaje zatrzymany, gdy odpowiedź na dane pytanie nie wyznacza kolejnego pytania. Metodologię CART charakteryzuje rekursywny podział binarny, a więc to, że węzeł macierzysty rozdzielany jest zawsze na dwa węzły potomne. Po dokonaniu podziałów, w każdej warstwie mierzony jest błąd klasyfikacji, a więc pewna niejednorodność kategorii wyniku.
2. Zalety zastosowania analizy CART
Metodologię CART charakteryzuje to, iż w większości przypadków wyniki otrzymane w postaci drzewa są łatwe w interpretacji. Bez wątpienia jest to jedna z ważniejszych zalet analizy CART. W różnych częściach powstałego w trakcie analizy drzewa, metoda ta wykorzystuje te same zmienne, co daje możliwość wskazania zależności między nimi. Ogromnym plusem tej metody jest posługiwanie się wszystkimi możliwymi kombinacjami zmiennych ciągłych i kategorialnych, dzięki czemu użytkownik nie traci czasu na przekodowywanie zmiennych. Zazwyczaj w metodach statystycznych przypadki zawierające braki danych nie są brane pod uwagę w analizie danych, co może prowadzić do otrzymania niewystarczająco dobrych wyników. Jednak metodę CART cechuje to, iż może być stosowana w zbiorach danych o licznych brakach danych. Kolejną zaletą tej analizy jest praca z wielowymiarowym wektorem danych, a także brak wymagań dotyczących założeń na temat związku zmiennej zależnej ze zmiennymi objaśniającymi.
3. Etapy analizy
-
Kryteria oceny trafności przewidywania:
Największą trafność ma model o najmniejszym koszcie klasyfikacji (w większości przypadków przyjmuje się za koszt stosunek przypadków błędnie sklasyfikowanych do wszystkich przypadków). -
Wybór podziału:
W każdym węźle drzewa wyszukiwany jest podział dający najlepszą trafność predykcji. Najczęściej w metodzie CART stosowane są następujące reguły podziałów: indeks Giniego, miara entropii i reguła podziału na dwie części. -
Warunek zatrzymania procesu podziału:
Rozszczepianie można przeprowadzać tak długo, aż uzyska się klasyfikację doskonałą. Jednak nie w tym celu stosuje się drzewa decyzyjne. Dlatego też w analizie określa się warunek zatrzymania procesu rozszczepiania. Dla kontroli tego procesu ustala się m.in. minimalną liczność węzłów. Wtedy proces podziału będzie tak długo przeprowadzany aż węzły końcowe będą jednorodne, bądź zawierać będą co najwyżej ustaloną liczbę przypadków. -
Ustalenie „wielkości” drzewa:
Dobór właściwego rozmiaru drzewa stanowi istotny problem metody CART. Z jednej strony drzewo powinno być jak najprostsze, ale z drugiej strony powinno też prezentować złożoność danych.
Z pojęciem „właściwego” rozmiaru drzewa łączą się terminy nadmiernego rozrostu jak i przycinania. W tym celu budowany jest model o maksymalnej liczbie liści, a następnie pewne fragmenty drzewa są usuwane tak, by wzrost błędu klasyfikacji był jak najmniejszy. Przycinanie pozwala na porównanie obu modeli, tj. modelu rozbudowanego i modelu zredukowanego i wybór takiego modelu zredukowanego, dla którego różnica między błędem klasyfikacji drzewa rozbudowanego a zredukowanego jest jak najmniejsza.
Zastosowanie metody CART
Poniżej przedstawiono analizę obserwacji pasażerów Titanica dokonanej przy pomocy programu Statistica w oparciu o dane zawarte w jednym z arkuszy programu (Titanic). Danego pasażera charakteryzują cztery zmienne, mianowicie: klasa, wiek, płeć oraz przeżycie. Zmienna zależna określona jest tutaj poprzez przeżycie katastrofy. Zmienne niezależne zaś to wiek, płeć oraz klasa.
Rozpoczynając analizę wybieramy moduł Data Mining}, a w zakładce Drzewa - C\&RT. Kolejny krok polega na wyborze zmiennych, ustaleniu podziału oraz kryterium zatrzymania. W celu otrzymania jak najlepszych wyników warto jest przetestować różne opcje.
W poniższej analizie jako dobroć dopasowania przyjęto miarę Giniego, a warunek stopu - minimalna liczność równą 40.
W poniższej analizie jako dobroć dopasowania przyjęto miarę Giniego, a warunek stopu - minimalna liczność równą 40.
Łatwo można zauważyć, że w większości przypadków pasażarowie nie przeżyli katastrofy statku. Informuje o tym rozkład zmiennej przedstawionej w węźle macierzystym - korzeniu drzewa. Spośród wszystkich zmiennych niezależnych, do podziału pierwszego węzła posłużyła zmienna określająca płeć pasażerów. Do lewego węzła przyporządkowano kobiety (liczebność klasy: 470 przypadków), a do prawego mężczyzn (liczbność klasy: 1731 przypadków). Drugi etap podziału wykorzystuje już dwie zmienne: węzeł o nazwie kobiety podzielono ze względu na klasy, a węzeł mężczyźni ze względu na wiek. Wielkość drzewa wynosi 5, co oznacza, że drzewo składa się z pięciu węzłów końcowych, które można opisac według nastepującego wzorca: jeśli ..., to ..., np. jeśli pasażerem była kobieta płynąca trzecią klasą, to nie przeżyła katastrofy.
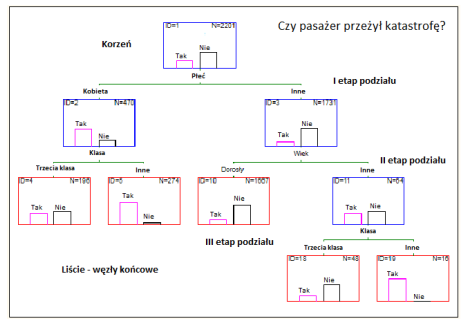
Rysunek 4: Zastosowanie metody CART
Literatura
[1] Breiman L., Friedman J.H., Olshen R.A., Stone C.J.; Classification and Regression Trees; Chapman and Hall; 1993.
[2] https://www.salford-systems.com/resources/whitepapers/116-an-overview-of-the-cart-methodology
[3] Timofeev R.; Classification and Regression Trees (CART). Theory and Applications; Berlin; 2004.
[2] https://www.salford-systems.com/resources/whitepapers/116-an-overview-of-the-cart-methodology
[3] Timofeev R.; Classification and Regression Trees (CART). Theory and Applications; Berlin; 2004.
Ekspert ds statystyki i baz danych
dr Marian Płaszczyca
Head of Statistics & IT
BioStat® sp. z o.o.



 Kontakt
Kontakt






 (+48) 666069834
(+48) 666069834
 statystyka@biostat.com.pl
statystyka@biostat.com.pl




