Analiza składowych głównych (PCA)
Analiza składowych głównych (PCA) służy m.in. do redukcji liczby zmiennych opisujących zjawiska, czy do odkrycia prawidłowości między zmiennymi. Polega ona na wyznaczeniu składowych będących kombinacją liniową badanych zmiennych. Dokładna analiza składowych głównych umożliwia wskazanie tych zmiennych początkowych, które mają duży wpływ na wygląd poszczególnych składowych głównych czyli tych, które tworzą grupę jednorodną. Składowa główna (u której wariancja jest zmaksymalizowana) jest wówczas reprezentantem tej grupy.
Kolejne składowe:
- są wzajemnie nieskorelowane,
- są definiowane tak, aby zmaksymalizować zmienność, która nie została wyjaśniona przez poprzednią składową,
Liczba składowych jest mniejsza lub równa liczbie zmiennych początkowych. Wariancja składowej głównej jest równa -tej co do wielkości wartości własnej macierzy Całkowita wariancja układu jest równa (gdzie dla są wszystkimi wartościami własnymi macierzy . Dzięki temu możemy zdefiniować część wariancji dla -tej składowej według wzoru:
.
Każda składowa główna wyjaśnia pewną część zmienności zmiennych początkowych.
Główne zastosowania analizy składowych głównych to:
- redukcja liczby zmiennych,
- wykrywanie struktury w związkach między zmiennymi,
- weryfikacja wykrytych prawidłowości i powiązań,
- klasyfikacja obiektów w nowych przestrzeniach zdefiniowanych przez utworzone czynniki.
Przykład
Załóżmy, że w losowo wybranej grupie osób pobraliśmy pięć pomiarów w różnych jednostkach pomiarowych. Ze względu na nieporównywalność danych, analizę składowych głównych wykonujemy w oparciu o macierz korelacji
Następnie liczymy wartości własne i wektory własne macierzy Otrzymujemy następujący wyniki:
- wartości własne:
- macierz wektorów własnych, w której kolumny zawierają współczynniki kolejnych składowych głównych:
|
|
|
|
|
|
|
|---|---|---|---|---|---|
|
|
0,51 |
0,30 |
0,72 |
-0,35 |
0,05 |
|
|
0,59 |
0,03 |
-0,08 |
0,67 |
-0,44 |
|
|
0,58 |
0,02 |
-0,65 |
-0,43 |
0,25 |
|
|
0,07 |
-0,69 |
0,08 |
-0,41 |
-0,59 |
|
|
0,21 |
-0,66 |
0,22 |
0,28 |
0,63 |
Dodatkowo liczymy wariancje składowej głównej :
|
Wartość własna |
Procent wariancji |
Skumulowany procent wariancji |
|---|---|---|
|
2,51 |
50,14% |
50,14% |
|
1,96 |
39,21% |
89,35% |
|
0,27 |
5,30% |
94,65% |
|
0,23 |
4,60% |
99,26% |
|
0,04 |
0,74% |
100,00% |
Obliczamy ładunki czynnikowe:
|
|
|
|
|
|
|
|---|---|---|---|---|---|
|
|
0,81 |
0,42 |
0,37 |
-0,17 |
0,01 |
|
|
0,94 |
0,04 |
-0,04 |
0,32 |
-0,08 |
|
|
0,92 |
0,03 |
-0,33 |
-0,20 |
0,05 |
|
|
0,11 |
-0,97 |
0,04 |
-0,20 |
-0,11 |
|
|
0,33 |
-0,92 |
0,11 |
0,14 |
0,12 |
oraz współczynniki determinacji :
|
|
|
|
|
|
|
|---|---|---|---|---|---|
|
|
0,66 |
0,17 |
0,14 |
0,03 |
0,00 |
|
|
0,89 |
0,00 |
0,00 |
0,10 |
0,01 |
|
|
0,84 |
0,00 |
0,11 |
0,04 |
0,00 |
|
|
0,01 |
0,94 |
0,00 |
0,04 |
0,01 |
|
|
0,11 |
0,85 |
0,01 |
0,02 |
0,01 |
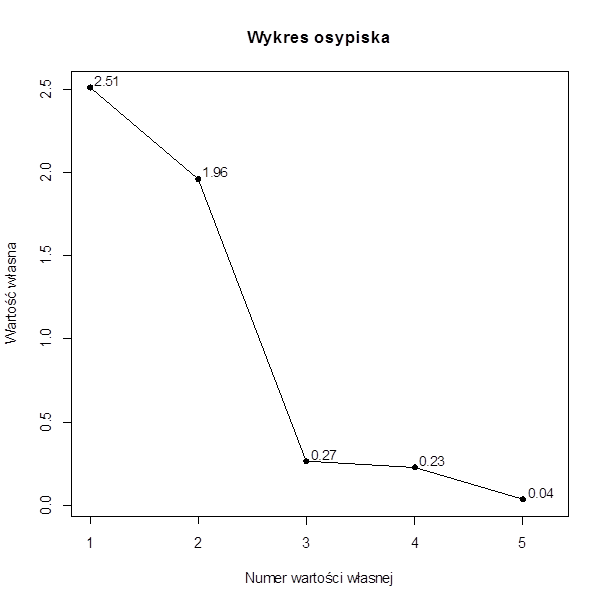
Do wyboru składowych głównych, posłużymy się wykresem osypiska. Jak widać na poniższym wykresie, osypiskiem czynnikowym są dwie ostanie wartości własne, więc wybieramy z całą pewnością dwie pierwsze składowe główne oraz uzyskalibyśmy w tedy 89,35% wyjaśnienia całkowitej wariancji (z tabeli powyżej). Składowa główna nie będzie brana pod uwagę, gdyż otrzymamy zadowalający podział zmiennych na dwie grupy reprezentowane przez oraz
Podział ten wynika z obliczonych ładunków czynnikowych oraz współczynników determinacji. Ładunki czynnikowe dla trzech pierwszych zmiennych są największe dla pierwszej składowej głównej, a dwie ostatnie zmienne są dobrze skorelowane z drugą składowa główną. Obie składowe wyjaśniają powyżej 80% wariancji zmiennych.
Wyniki uzyskano stosując środowisko obliczeniowe R



 Kontakt
Kontakt





 (+48) 666069834
(+48) 666069834
 statystyka@biostat.com.pl
statystyka@biostat.com.pl




