Test normalności Shapiro-Wilka

Test Shapiro-Wilko jest uznawany za najlepszy test do sprawdzenia normalności rozkładu zmiennej losowej. Głównym atutem tego testu jest jego duża moc, tzn. dla ustalonego α prawdopodobieństwo odrzucenia hipotezy H₀, jeśli jest ona fałszywa, jest większe niż w przypadku innych tego typu testów.

Hipotezy zerowa oraz alternatywna są następującej postaci:

H₀: Rozkład badanej cechy jest rozkładem normalnym.

H₁: Rozkład badanej cechy nie jest rozkładem normalnym.

Załóżmy, że pobrano próbę $X_1,\ldots, X_n$. Porządkując próbę niemalejąco otrzymamy statystyki pozycyjne $\tilde{X_1},\ldots, \tilde{X_n}$.

Statystyka testowa dla testu Shapiro-Wilka zadana jest wzorem:

$W=\frac{\left( \sum\limits^{\lfloor \frac{n}{2}\rfloor }_{i=1} a_i(n)\left( \widetilde{X}_{n-i+1}-\widetilde{X}_i\right) \right)^2}{\sum\limits_{i=1}^n\left( X_i-\bar{X} \right)^2}$

gdzie współczynniki $a_i(n)$ są stablicowanymi współczynnikami testu dla liczności próby n.Wartość krytyczną dla ustalonego $\alpha$ odczytujemy z tablic kwantyli $W(\alpha,n)$ do testu Shapiro-Wilka. Obszar krytyczny w tym teście jest obszarem lewostronnym, a zatem hipotezę zerową odrzucamy, jeżeli wyliczona wartość statystyki testowej jest mniejsza bądź równa wartości krytycznej, tzn. $W \leq W(\alpha,n)$.

Zebrano i posortowano niemalejąco 20 obserwacji charakteryzujących wskaźnik masy ciała (BMI)
badanych pacjentów. Aby przeprowadzić analizę statystyczną musimy dowiedzieć się, czy rozkład tej
cechy jest rozkładem normalnym.

 

BMI = [21, 7; 22, 5; 23, 1; 23, 6; 24, 2; 24, 5; 24, 6; 25, 5; 25, 7; 25, 9; 26, 2; 26, 4; 27, 1;

27, 3; 27, 3; 27, 7; 28, 1; 30, 4; 30, 7; 31, 2]

Aby obliczyć wartość statystyki testowej dla testu Shapiro-Wilka musimy wyznaczyć następujące wartości:

 

$\overline{x} = \frac{21,7+\dots+31,2}{20} = 26,185$

$\sum\limits^{20}_{i=1}(x_{i} - \overline{x})^2 = (21,7 - 26,185)^{2} + \dots + (31,2 - 26,185)^{2} = 132,6055$

Statystyka testowa $W$ przyjmie zatem wartość:

$W = \frac{128,2703}{132,6055} \approx 0,9673$

Dla $\alpha = 0, 05$ i dla $n = 20$, stablicowana wartość krytyczna wynosi $W(0, 05; 20) = 0, 905$. A zatem zachodzi
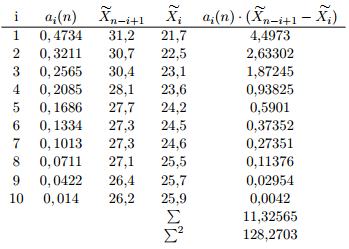
nierówność $W > W(\alpha, n)$, co oznacza, że nie ma podstaw do odrzucenia hipotezy o normalności
rozkładu badanych danych.

Ekspert ds statystyki i baz danych

dr Marian Płaszczyca

Head of Statistics & IT

BioStat^® sp. z o.o.

(+48) 666069834
statystyka@biostat.com.pl

Pomóż nam rozwijać serwis z materiałami edukacyjnymi. Polub nas na Facebook.

Udostępnij